The Heptagon, p2, p3
…through words, through touch, and simply by the fact of our existence; we are accessible to the sensory organs of our fellow humans. For me, this is where the heptagon comes in. A heptagon possessing seven sides each the same length as the those of the hexagon will, with its one extra point, protude beyond the circle that surrounds the hexagon. The extra point acts like an egg-tooth, breaking the confines of the inner person to release it into the world outside; the world of the outer person, tangible to others.
A prevailing (and extremely subjective) popular spiritual belief is that the further we travel into our inner world, the closer we are to the real universe. Physical senses have not evolved to interpret the universe of energy, instead they exist to ensure our survival in the world of its appearance, which is in turn defined for us by the limits of our human senses. If simplicity is the most faithful mask of truth, it can be found in the very big, the very small, and—within the psyche—the very primal; in the nature of consciousness itself. Symbolically, this is the territory of the first few numbers; the 1, 2 and 3 for which most cultures share a similar set of symbols. 4 sits poised like a portal with its four-square 90° symmetry half-way between the acute angles at the corners of a regular triangle and the obtuse angles of every other regular polygon. 5, 6 and 7 are the first of those innumerable obtuse-angled polygons expanding ever-outwards towards infinity, and the difference between 6 and 7 is a neat symbol of the boundary between the inner, that which arises from within, and the outer or objective world, which we consider to be beyond the boundaries of the self. Geometrically, this boundary is represented by the circle that contains the hexagon, but not the heptagon. The heptagon can thus represent our capacity for reaching beyond the self towards the other, into whatever and whoever we consider to be not-us. The extra point, the extra side of the heptagon symbolises curiosity, exploration, touch, sex, inspiration, expression, any contact between the inner and the outer, any means by which our experience of the world beyond the self is increased. The person locked inside the circle of their inner life may possess remarkable qualities, but without interaction with the world they remain socially sterile. The heptagon is fertility, with a potency to affect the outer world by creating a medium of expression for the inner self, allowing others to appreciate (or not) what would otherwise remain purely subjective.
When, at the end of a life, the psyche collapses back through 5 and through the portal of 4 to 3 it becomes a stable, unmoving triangle, mind body and soul. At 2, it becomes a single line like the continual beep of a merciless heart monitor then, at 1, a point. When I die my visible self will collapse into a line that folds up into a single point like the white dot at the centre of an old TV. Point or line create nothing of themselves. Only when they are combined can they produce some kind of recognisable form, and the simplest forms are regular polygons. There are as many polygons as there are numbers, and the closer they approach infinity, the more completely they approximate the circle, without ever actually becoming circles; they can only be polygons no matter how many trillions upon trillions of sides they possess. Of all these polygons, the heptagon is the first to break free from the generative matrix of the circle, and at some fundamental level—because mathematics is the geometry of the natural world made visible and we all have running through every atom of our bodies something of that infinitely creative anima mundi—perhaps the cultural ascendancy of the number seven over the number six bears witness to this geometrical fact.
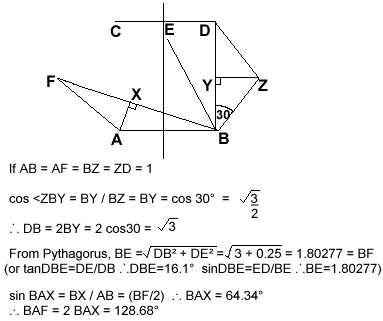
My proof, like my experience of the world, will never be complete. When mathematically checked the angles are within a fraction of a degree, and that’s not exact, but captivated by the symbolism, I persist in following that elusive meandering line towards a solution of Euclidian elegance that will prove its symmetry without resorting to the clumsiness of sines, cosines and the like.